Deterministische Endliche Automaten

Definition

Deterministisch → jedes Zeichen läst an jedem Zustand genau einen Folgezustand aus
Endlich → es gibt endlich viele Zustände und Zeichen

tip

Definiton von Automaten in der Tafelwerks-Ergänzung

DEA

ein DEA ist ein 5-Tupel Automat:

Z = Zustandsmenge
S = Alphabet
Z₀ = Startzustand aus Zustandsmenge
E = Endzustandsmenge
δ = Übergangsmenge, die für Zustände und zeichen einen Folgezustand angibt.

Bsp.:

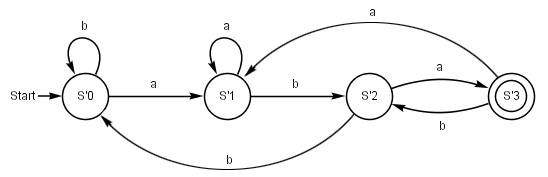
Z = (S0, S1, S2, S3)
S = (a, b)
Z₀ = (S0)
E = (S3)
δ = (S0, a → S1; S1, a → S1; usw...)

Akzeptor

Ein DEA wird als Akzeptor bezeichnet, sobald er eine formale Sprache insofern beschreibt, dass der Automat exakt bei Eingaben von Worten die der Grammatik entsprechen, den Endzustand erreicht.

danger

Begrenzung von DEA: können nicht beliebig weit zählen. DEA können nicht zahlen/ Werte merken. Problem bei aⁿbⁿ oder aᵐbⁿ n≠m

Mealy-Automat

(DEA mit Ausgabe)

ist ein 6-Tupel-Automat: OHNE ENDZUSTAND

Z = Zustandsmenge
S = Eingabealphabet
W = Ausgabealphabet
Z₀ = Startzustand aus Z
δ = Übergangsfunktion
λ = Ausgabefunktion → gibt für Zustande und Zeichen die erfolgende Ausgabe aus

Bsp.:

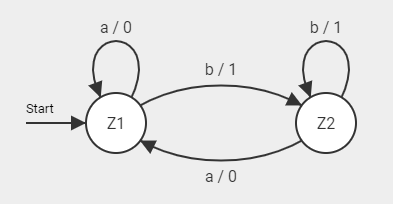
Z = (Z1, Z2)
S = (a, b)
W = (0, 1)
Z₀ = (Z1)
δ = (Z1, a → Z1; Z1, b → Z2; usw...)
λ = (Z1, a → 0; Z2, b → 1; usw...)

δ und λ können auch so dargestellt werden:

δ	a	b
Z1	Z1	Z2
Z2	Z1	Z2

λ	a	b
Z1	0	1
Z2	0	1

tip

Von umfangreicheren Modellen in dieser Schreibweise nicht erschrecken lassen!

Turing-Maschine

• hat aktives Element: Schreib-/ Lesekopf wogegen ein DEA eine Eingabe nur Schrittweise abarbeitet

ist ein 7-Tupel Automat

Z = Zustandsmenge
Σ = Eingabealphabet
Ω = Bandalphabet
Z₀ = Startzustand aus Z
δ = Übergangsfunktion
$ = Bandvorbeleungsszeichen
ZE = Menge aller Zustände

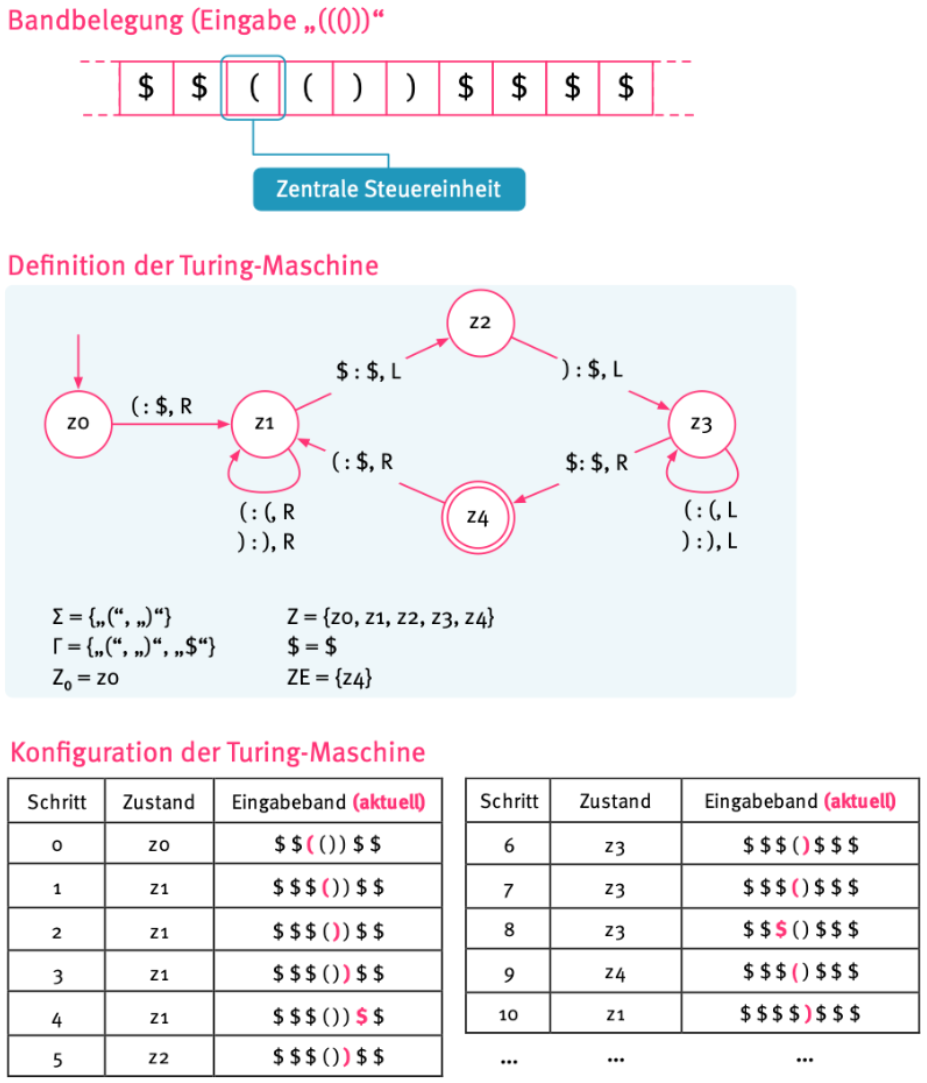
Z = (Z₀ , Z₁ , Z₂ , Z₃ , Z₄)
Σ = ("(", ")")
Ω = ("(", ")", "$")
$ = $ Z₀ = Z₀ ZE = Z₄

Bei einer Eingabe von "((()))", landet die Turing-Maschine im Endzustand mit nur $
Bei einer Eingabe von "(()))" in Z₂
Bei einer Eingabe von "()(()))" in Z₄